

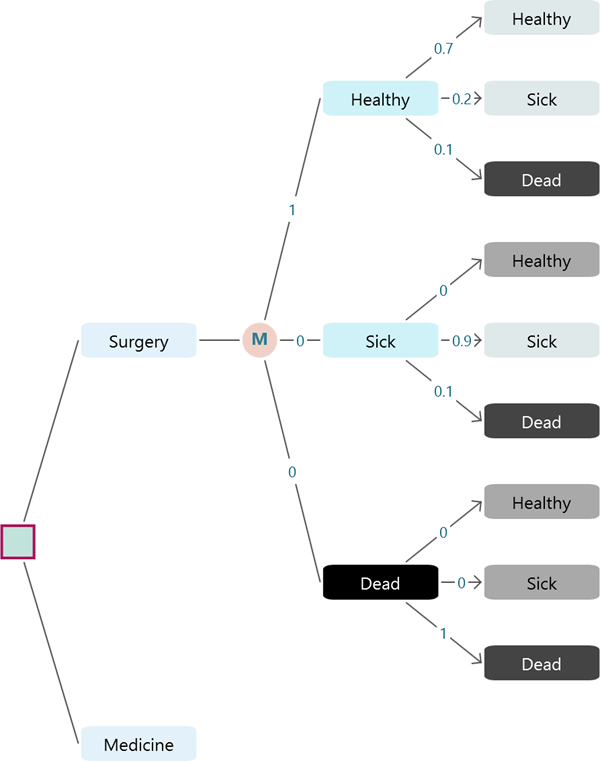
In such a diagram you can trace a pathway that defines a sequence of states-perhaps Because these numbers are probabilities, they must lie between 0 and 1, and all the probabilities issuing from a dot must add up to exactly 1. Each arrow has an associated number, which gives the probability of that transition. Dots represent states arrows indicate transitions. The aim of the algorithm is to calculate for each web page the probability that a reader following links at random will arrive at that page.Ī diagram made up of dots and arrows shows the structure of a Markov chain. For example, the PageRank algorithm devised by Larry Page and Sergey Brin, the founders of Google, is based on a Markov chain whose states are the pages of the World Wide Web-perhaps 40 billion of them. Recent years have seen the construction of truly enormous Markov chains. A realistic Monopoly model incorporating all of the game’s quirky rules would be much larger. For each state there are transitions to all other states that can be reached in a roll of the dice-generally those from 2 to 12 squares away. For Monopoly, the minimal model would require at least 40 states, corresponding to the 40 squares around the perimeter of the board. There are nine possible transitions (including “identity” transitions that leave the state unchanged). A simplified model of weather forecasting might have just three states: To be considered a proper Markov chain, a system must have a set of distinct states, with identifiable transitions between them. The events are linked, one to the next they form a Markov chain. The probabilities of future events depend on the current state of the system. From different starting points, the same number of steps could take you to the Boardwalk or put you in jail. Rolling the dice determines how many steps your token advances around the board, but where you land at the end of a move obviously depends on where you begin. Storms often last several days, so rain today may signal an elevated chance of rain tomorrow.įor another example where independence fails, consider the game of Monopoly. Suppose the probability of a rainy day is 1/3 it doesįollow that the probability of rain two days in a row is 1/3×1/3=1/9. However, not all aspects of life adhere to this convenient principle. , the joint probability of both events is the product More generally, if two independent events have probabilities If you toss a fair coin twice, the chance of seeing heads both times is simply 1/2×1/2, or 1/4. This principle of independence makes it easy to calculate compound probabilities. If the coin is fair, the probability of heads is always 1/2.
It’s an article of faith that one flip of a coin has no effect on the next. Probability theory has its roots in games of chance, where every roll of the dice or spin of the roulette wheel is a separate experiment, independent of all others. And the story unfolds amid the tumultuous events that transformed Russian society in the early years of the 20th century.īefore delving into the early history of Markov chains, however, it’s helpful to have a clearer idea of what the chains are and how they work. For added drama there’s a bitter feud between two forceful personalities.

It features an unusual conjunction of mathematics and literature, as well as a bit of politics and even theology. And Markov chains themselves have become a lively area of inquiry in recent decades, with efforts to understand why some of them work so efficiently-and some don’t.Īs Markov chains have become commonplace tools, the story of their origin has largely faded from memory. In statistics, the chains provide methods of drawing a representative sample from a large set of possibilities. In physics the Markov chain simulates the collective behavior of systems made up of many interacting particles, such as the electrons in a solid. Methods not too different from those Markov used in his study of Pushkin help identify genes in DNA and power algorithms for voice recognition and web search. Markov chains are everywhere in the sciences today.


 0 kommentar(er)
0 kommentar(er)
